E.1 Psychology’s replication crisis
What happens with a scientific discipline if it predominantly fails to replicate99 previous discoveries? This question frequently arose after a groundbreaking project revealed that psychology is facing a replication crisis. In 2011, the Open Science Collaboration (2015) launched a large-scale project – the so-called “Reproducibility Project” – in which they attempted 100 direct replications of experimental and correlational studies in psychology. The results are worrisome: 97% of the original studies reported statistically significant results, whereas the initiative could merely replicate 36% of the results.100 This low replicability rate, however, does not imply that about two-thirds of the discoveries are wrong. It emphasizes that research outcomes should not be taken at face value but scrutinized by the scientific community. Most of all, the results show that scientists should take action to increase the replicability of their studies. This urgent need is further fueled by the discovery that the prevalence of low replicability rates diminishes the public’s trust (e.g., Wingen, Berkessel, and Englich 2019) and, in the long run, might undermine the credibility of psychology as a science.
In order to know how to increase a study’s replicability, it is crucial to investigate what causes replications to fail. Essentially, failing to replicate the significant results of the original study has three roots: The original study yielded a false-positive, the replication study yielded a false-negative, or too divergent methodologies led to two different outcomes (Open Science Collaboration 2015). We focus here on false-positives and diverging methodologies. We only briefly touch on false-negatives in the replication study when we talk about low statistical power.
E.1.1 Publication bias, QRP’s, and false-positives
Weighing evidence in favor of verifying preconceptions and beliefs rather than falsifying them is a cognitive bias (confirmation bias). This natural form of reasoning can be a considerable challenge in doing proper research, as the full amount of information should be taken into account and not just those consistent with prior beliefs. Confirmation bias also manifests itself in a tendency to see patterns in the data and perceive meaning, when there is only noise (apophenia) and overestimating the prediction of an event after it occurred, typically expressed as “I knew it all along!” (hindsight bias).
These biases further pave the way for a skewed incentive structure that prefers confirmation over inconclusiveness or contradiction. In psychological science, there is a vast prevalence of publications that report significant (\(p < 0.05\)) and novel findings in contrast to null-results (e.g., Sterling 1959) or replication studies (e.g., Makel, Plucker, and Hegarty 2012). This substantial publication bias towards positive and novel results may initially seem entirely plausible. Journals might want to publish flashy headlines that catch the reader’s attention rather than “wasting” resources for studies that remain inconclusive. Furthermore, scientific articles that report significant outcomes are more likely to be cited (Duyx et al. 2017) and thus may increase the journal’s impact factor (JIF). Replication studies might not be incentivized because they are considered tedious and redundant. Why publish results that don’t make new contributions to science?101
Publication bias operates at the expense of replicability and thus the reliability of science. The pressure of generating significant results can further fuel the researcher’s bias (Fanelli 2010). Increasing cognitive biases towards the desired positive result could therefore lead researchers to draw false conclusions. To cope with this “Publish or Perish” mindset, researchers may increasingly engage in questionable research practices (QRP’s) as a way of somehow obtaining a \(p\)-value less than the significance level \(\alpha\). QRP’s fall into the grey area of research and might be the norm in psychological science. Commonly researchers “\(p\)-hack” their way to a significant \(p\)-value by analyzing the data multiple ways through exploiting the flexibility in data collection and data analysis (researcher degrees of freedom). This exploratory behavior is frequently followed by selective reporting of what “worked”, so-called cherry-picking. Such \(p\)-hacking also takes on the form of unreported omission of statistical outliers and conditions, post hoc decisions to analyze a subgroup, or to change statistical analyses. Furthermore, researchers make rounding errors by reporting their results to cross the significance threshold (.049 becomes .04), they randomly stop collecting data when the desired \(p\)-value of under .05 pops up, or they present exploratory hypotheses102 as being confirmatory (HARKing, Hypothesizing After the Results are Known).
Diederik Stapel, a former professor of social psychology at Tilburg University, writes in his book Faking Science: A True Story of Academic Fraud about his scientific misconduct. He shows how easy it is to not just fool the scientific community (in a discipline where transparency is not common practice) but also oneself:
I did a lot of experiments, but not all of them worked. […] But when I really believed in something […] I found it hard to give up, and tried one more time. If it seemed logical, it must be true. […] You can always make another couple of little adjustments to improve the results. […] I ran some extra statistical analyses looking for a pattern that would tell me what had gone wrong. When I found something strange, I changed the experiment and ran it again, until it worked (Stapel 2014, 100–101).
If the publication of a long-standing study determines whether researchers get funding or a job, it is perfectly understandable why they consciously or subconsciously engage in such practices. However, exploiting researcher degrees of freedom by engaging in QRP’s poses a significant threat to the validity of the scientific discovery by blatantly inflating the probability of false-positives. By not correcting the significance threshold accordingly, many analyses are likely to be statistically significant just by chance, and reporting solely those that “worked” additionally paints a distorted picture on the confidence of the finding.

Example. Let’s illustrate \(p\)-hacking based on a popular comic by xkcd. In the comic, two researchers investigate whether eating jelly beans causes acne. A \(p\)-value larger than the conventional \(\alpha\)-threshold doesn’t allow them to reject the null hypothesis of no effect. Well, it must be one particular color that is associated with acne. The researchers now individually test the 20 different colors of jelly beans. Indeed, numerous tests later, they obtain the significant \(p\)-value that they have probably been waiting for. The verdict: Green jelly beans are associated with acne! Of course, this finding leads to a big headline in the newspaper. The article reports that there is only a 5% chance that the finding is due to coincidence.
However, the probability that the finding is a fluke is about 13 times higher than anticipated and reported in the paper. Let’s check what happened here:
In the first experiment (without color distinctions), there was a \(5\%\) chance of rejecting \(H_0\), and consequently a \(95\%\) chance of failing to reject \(H_0\). Since the \(\alpha\)-level is the upper bound on a false-positive outcome, the confidence in the finding reported in the newspaper would have been true if the researchers had kept it with just one hypothesis test. However, by taking the 20 different colors into account, the probability of obtaining a non-significant \(p\)-value in each of the 20 tests dropped from \(95\%\) to \(0.95^{20} \approx 35.85\%\), leaving room for a \(64.15\%\) chance that at least one test yielded a false-positive. The probability of at least one false-positive due to conducting multiple hypothesis tests on the same data set is called the family-wise error rate (FWER). Formally, it can be calculated like so:
\[\alpha_{FWER} = 1 - (1 - \alpha)^n,\]
where \(\alpha\) denotes the significance level for each individual test, which is conventionally set to \(\alpha = 0.05\), and \(n\) the total number of hypothesis tests.
Conducting multiple tests on the same data set and not correcting the family-wise error rate accordingly, therefore makes it more likely that a study finds a statistically significant result by coincidence.
To investigate how prevalent QRP’s are in psychological science, Leslie John et al. (John, Loewenstein, and Prelec 2012) surveyed over 2000 psychologists regarding their engagement in QRP’s. They found that 66.5% of the respondents admitted that they failed to report all dependent measures, 58% collected more data after seeing whether the results were significant, 50% selectively reported studies that “worked”, and 43.4% excluded data after looking at the impact of doing so. Based on the self-admission estimate, they derived a prevalence estimate of 100% for each mentioned QRP. These numbers once more reinforce the suspicion that QRP’s are the norm in psychology. Together with the fact that these practices can blatantly inflate the false-positive rates, one might conclude that much of the psychological literature cannot be successfully replicated and thus might be wrong.
E.1.2 Low statistical power
Another factor that can account for unreliable discoveries in the scientific literature is the persistence of highly underpowered studies in psychology (e.g., Cohen 1962; Sedlmeier and Gigerenzer 1989; Marjan, Dijk, and Wicherts 2012; Szucs and Ioannidis 2017). A study’s statistical power is the probability of correctly rejecting a false null hypothesis, i.e., the ideal in NHST. Defined as \(1 − \beta\), power is directly related to the probability of encountering a false-negative, meaning that low-powered studies are less likely to reject \(H_0\) when it is in fact false. Figure E.1 shows the relationship between \(\alpha\)-errors and \(\beta\)-errors (slightly adapted from a previous figure in Chapter 16.4), as well as the power to correctly rejecting \(H_0\).
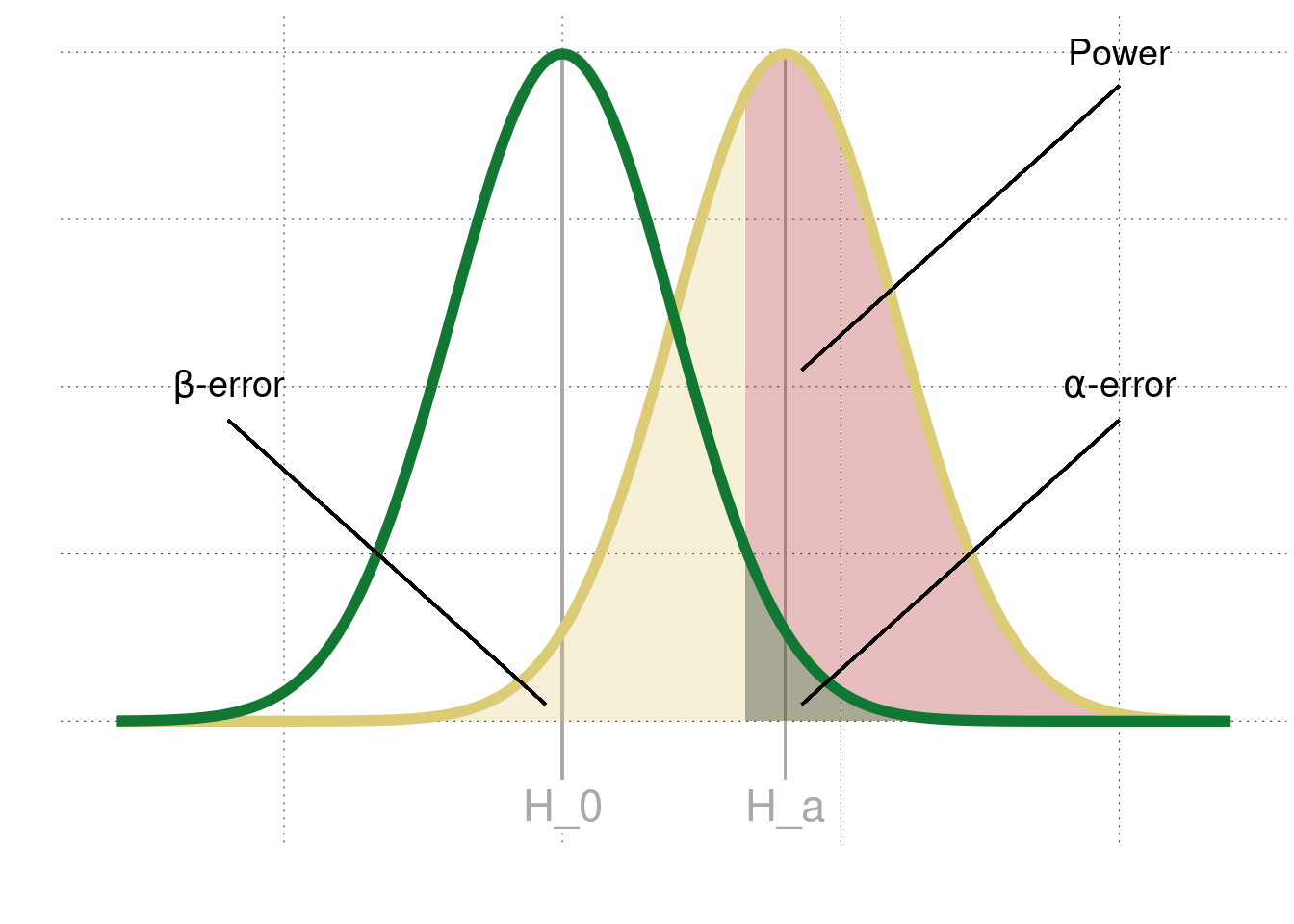
Figure E.1: Relationship between power, \(\alpha\) and \(\beta\)-errors.
It may be tempting to conclude that a statistically significant result of an underpowered study is “more convincing”. However, low statistical power also decreases the probability that a significant result reflects a true effect (that is, that the detected difference is really present in the population). This probability is referred to as the Positive Predictive Value (PPV). The PPV is defined as \[PPV = \frac{(1 - \beta) \cdot R}{(1 - \beta) \cdot R + \alpha},\] where \(1 − \beta\) is the statistical power, \(R\) is the pre-study odds (the odds of the prevalence of an effect before conducting the experiment), and \(\alpha\) is the type I error. Choosing the conventional \(\alpha\) of 5% and assuming \(R\) to be 25%, the PPV for a statistically significant result of a study with 80% power - which is deemed acceptable - is 0.8. If the power is reduced to 35%, the PPV is 0.64. A 64% chance that a discovered effect is true implies that there is a 36% chance that a false discovery was made. Therefore, low-powered studies are more likely to obtain flawed and unreliable outcomes, which contribute to the poor replicability of discoveries in the scientific record.
Another consequence of underpowered studies is the overestimation of effect sizes103 and a higher probability of an effect size in the wrong direction. These errors are referred to as Type M (Magnitude) and Type S (Sign) errors, respectively (Gelman and Carlin 2014). If, for example, the true effect size (which is unknown in reality) between group \(A\) and \(B\) is 20 ms, finding a significant effect size of 50 ms would overestimate the true effect size by a factor of 2.5. If we observe an effect size of -50 ms, we would even wrongly assume that group \(B\) performs faster than group \(A\).
The statistical power, as well as Type S and Type M error rates can be easily estimated by simulation. Recall the example from Chapter 16.6.3, where we investigated whether the distribution of IQ’s from a sample of CogSci students could have been generated by an average IQ of 100, i.e., \(H_0: \mu_{CogSci} = 100 \ (\delta = 0)\). This time, we’re doing a two-tailed \(t\)-test, where the alternative hypothesis states that there is a difference in means without assigning relevance to the direction of the difference, i.e., \(H_a: \mu_{CogSci} \neq 100 \ (\delta \neq 0)\). We plan on recruiting 25 CogScis and set \(\alpha = 0.05\).
Before we start with the real experiment, we check its power, Type S, and Type M error rates by hypothetically running the same experiment 10000 times in the WebPPL code box below. From the previous literature, we estimate the true effect size to be 1 (CogScis have an average IQ of 101) and the standard deviation to be 15. Since we want to know how many times we correctly reject the null hypothesis of equal means, we set the estimated true effect size as ground truth (delta variable) and sample from \(Normal(100 + \delta, 15)\). Variable t_crit stores the demarcation point for statistical significance in a \(t\)-distribution with n - 1 degrees of freedom.
We address the following questions:
- If the true effect size is 1, what is the probability of correctly rejecting the null hypothesis of equal means (= an effect size of 0)?
- If the true effect size is 1, what is the probability that a significant result will reflect a negative effect size (that is, an average IQ of less than 100)?
- If the true effect size is 1 and we obtain a statistically significant result, what is the ratio of the estimated effect size to the true effect size (exaggeration ratio)?
Play around with the parameter values to get a feeling of how power can be increased. Remember to change the t_crit variable when choosing a different sample size. The critical \(t\)-value can be easily looked up in a \(t\)-table or computed with the respective quantile function in R (e.g, qt(c(0.025,0.975), 13) for a two-sided test with \(\alpha = 0.05\) and \(n = 14\)). For \(n \geq 30\), the \(t\)-distribution approximates the standard normal distribution.
var delta = 1; // true effect size between mu_CogSci and mu_0
var sigma = 15; // standard deviation
var n = 25; // sample size per experiment
var t_crit = 2.063899; // +- critical t-value for n-1 degrees of freedom
var n_sim = 10000; // number of simulations (1 simulation = 1 experiment)
///fold:
var se = sigma/Math.sqrt(n); // standard error
// Effect size estimates:
/* In each simulation, drep(n_sim) takes n samples from a normal distribution
centered around the true mean and returns a vector of the effect sizes */
var drep = function(n_sim) {
if(n_sim == 1) {
var sample = repeat(n, function(){gaussian({mu: 100 + delta, sigma: sigma})});
var effect_size = [_.mean(sample)-100];
return effect_size;
} else {
var sample = repeat(n, function(){gaussian({mu: 100 + delta, sigma: sigma})});
var effect_size = [_.mean(sample)-100];
return effect_size.concat(drep(n_sim-1));
}
}
// vector of all effect sizes
var ES = drep(n_sim);
// Power:
/* get_signif(n_sim) takes the number of simulations and returns a vector of only
significant effect sizes. It calculates the absolute observed t-value, i.e.,
|effect size / standard error| and compares it with the critical t-value. If the
absolute observed t-value is greater than or equal to the critical t-value, the
difference in means is statistically significant.
Note that we take the absolute t-value since we're conducting a two-sided t-test and
therefore also have to consider values that are in the lower tail of the sampling
distribution. */
var get_signif = function(n_sim) {
if(n_sim == 1) {
var t_obs = Math.abs(ES[0]/se);
if(t_obs >= t_crit) {
return [ES[0]];
} else {
return [];
}
} else {
var t_obs = Math.abs(ES[n_sim-1]/se);
if(t_obs >= t_crit) {
return [ES[n_sim-1]].concat(get_signif(n_sim-1));
} else {
return [].concat(get_signif(n_sim-1));
}
}
}
// vector of only significant effect size estimates
var signif_ES = get_signif(n_sim);
// proportion of times where the null hypothesis would have been correctly rejected
var power = signif_ES.length/n_sim;
// Type S error:
/* get_neg_ES(n_sim) takes the number of simulations and returns a vector of
significant effect sizes that are negative. */
var get_neg_ES = function(n_sim){
if(n_sim == 1){
if(signif_ES[n_sim-1] < 0){
return [signif_ES[n_sim-1]];
} else {
return [];
}
} else {
if(signif_ES[n_sim-1] < 0){
return [signif_ES[n_sim-1]].concat(get_neg_ES(n_sim-1));
} else {
return [].concat(get_neg_ES(n_sim-1));
}
}
}
// vector of only significant effect size estimates that are negative
var neg_ES = get_neg_ES(n_sim);
/* If at least one simulation yielded statistical significance, calculate the
proportion of significant+negative effect sizes to all significant effect sizes. */
var type_s = function(){
if(signif_ES.length == 0) {
return "No significant effect size";
} else {
return neg_ES.length/signif_ES.length;
}
}
// proportion of significant results with a negative effect size
var s = type_s();
// Type M error:
// take the absolute value of all significant effect sizes
var absolute_ES = _.map(signif_ES, Math.abs);
/* If at least one simulation yielded statistical significance, calculate the
ratio of the average absolute effect size to the true effect size. */
var type_m = function(){
if(signif_ES.length == 0) {
return "No significant effect size";
} else {
return _.mean(absolute_ES)/delta;
}
}
// exaggeration ratio
var m = type_m();
// Results:
// print results
display("Power: " + power +
"\nType II error: " + (1-power) +
"\nType S error: " + s +
"\nType M error: " + m
);
// print interpretation depending on results
if(power != 0) {
if(_.round(m,1) == 1) {
display(
"Interpretation:\n" +
// Power
"If the true effect size is " + delta + ", there is a " +
_.round((power*100),1) + "% chance of detecting a significant \ndifference. "+
// Type S error
"If a significant difference is detected, there is a " +
_.round((s*100),1) +
"% chance \nthat the effect size estimate is negative. " +
// Type M error
"Further, the absolute estimated effect size is expected to be about the " +
"same as the true effect size of " + delta + "."
);
} else {
display(
"Interpretation:\n" +
// Power
"If the true effect size is " + delta + ", there is a " +
_.round((power*100),1) + "% chance of detecting a significant \ndifference. "+
// Type S error
"If a significant difference is detected, there is a " +
_.round((s*100),1) +
"% chance \nthat the effect size estimate is negative. " +
// Typ M error
"Further, the absolute estimated effect size is expected to be " +
_.round(m,1) + " times too high."
);
}
} else {
display(
"Interpretation:\n" +
// Power
"If the true effect size is " + delta + ", there is no " +
"chance of detecting a significant \ndifference at all. " +
"Since Type S and Type M errors are contingent on a \nsignificant " +
"result, there is no chance of having them in this case."
);
}
///
As the power of replication studies is typically based on the reported effect size of the original study, an inflated effect size also renders the power of the replication study to be much lower than anticipated. Hence, an underpowered study may additionally increase the replications’ probability of encountering a type II error, which may lead replicators to misinterpret the statistical significance of the original study as being a false-positive. Besides being self-defeating for authors of the original study, this may compromise the veracity of the cumulative knowledge base that direct replications aim to build.
E.1.3 Lack of transparency
When it comes to the reporting of methodologies, there seem to be disagreements within the scientific community. In his new Etiquette for Replication, Daniel Kahneman (2014) called for new standards for conducting direct replication studies. Concretely, replicators should be obliged to consult the authors of the original study – otherwise, the replication should not be valid. According to him, the described methodologies in psychology papers are too vague to permit direct replications. He argues that “[…] behavior is easily affected by seemingly irrelevant factors” and that paraphrasing experimental instructions discards crucial information, as “[…] their wording and even the font in which they are printed are known to be significant”. Kahneman’s proposed rules for the interaction between authors and replicators led to heated discussions within the discipline. Chris Chambers (2017, 52–55) refers to several responses to Kahneman, among others, from psychologist Andrew Wilson. In his blog post, titled Psychology’s real replication problem: our Methods sections, he takes an unequivocal stand on rejecting rigid standards for replication studies:
If you can’t stand the replication heat, get out of the empirical kitchen because publishing your work means you think it’s ready for prime time, and if other people can’t make it work based on your published methods then that’s your problem and not theirs (Wilson 2014).
Of course, there are also voices between those extremes that, even if they disagree with Kahneman’s proposal, agree that there are shortcomings in reporting methodologies. So why are method sections not as informative as they should be? A reason might be that the trend towards disregarding direct replications – due to lacking incentives – decreases the importance of detailed descriptions about the experimental design or data analyses. Furthermore, editors may favor brief method descriptions due to a lack of space in the paper. To minimize a variation in methodologies that might account for different outcomes, it is essential that journal policies change accordingly.
In addition to detailed reporting of methodologies, further materials such as scripts and raw data are known to facilitate replication efforts. In an attempt to retrieve data from previous studies, Hardwicke and Ioannidis (2018) encountered that almost 40% of the authors did not respond to their request in any form, followed by almost 30% not willing to share their data. The reluctance to share data for reanalysis can be related to weaker evidence and more errors in reporting statistical results (Wicherts, Bakker, and Molenaar 2011). This finding further intensifies the need for assessing the veracity of the reported results by reanalyzing the raw data, i.e., checking its computational reproducibility. However, computational replication attempts can hardly be conducted without transparency of the original study. To end this vicious circle and make sharing common practice, journals could establish mandatory sharing policies or provide incentives for open practices.
References
Direct replication is the repetition of an experiment as close as possible to the original methodology. A replication attempt is declared to be “successful” if it was capable of obtaining the same results as the original experiment on the new data set. Replicability is often interchangeably used with reproducibility, which is the ability to obtain the same results as the original experiment on the original data set.↩︎
There are several methods to assess the replicability of a study result. The Reproducibility Project separately evaluated the replication success – among others – based on (a) statistical significance (\(p < 0.05\)) (b) inclusion of original effect sizes within the 95% CI of replication effect sizes (c) magnitude between effect sizes (d) subjective assessment (“Did it replicate?”). Here, replication success is only evaluated based on statistical significance.↩︎
This way of thinking might be the reason why direct replications were virtually replaced by conceptual replications, which is the replication of a basic idea from previous research, albeit with different experimental methods to preserve novelty.↩︎
An exploratory hypothesis is one that was generated after the data was inspected, that is, explored for unanticipated patterns. In contrast, a confirmatory hypothesis is one that is defined before data collection. Both types are essential for scientific progress: Theories are generated by exploring the data and tested as confirmatory hypotheses in a new experiment. However, it gets fraudulent when serendipitous findings are passed off as being predicted in advance.↩︎
The effect size quantifies the difference between two variables (e.g., the difference in means) or the strength of the relationship between two variables (e.g., correlation coefficient). While statistical significance attests that there is an effect, the effect size tells us something about the magnitude of the effect (also called practical significance).↩︎