theory

• posterior inference & credible values

• Bayes factors & model comparison

• comparison of Bayesian and "classical" NHST

practice

• basics of MCMC sampling

• tools for BDA ( JAGS, Stan, WebPPL, Jasp, rstanarm)

• Bayesian cognitive modeling example

• Markov Chain Monte Carlo methods
  • Metropolis Hastings
  • Gibbs
  • Hamiltonian MC
• convergence / representativeness
  • trace plots
  • \(\hat{R}\)
• efficiency
  • autocorrelation
  • effective sample size

Bayes rule for data analysis:

\[\underbrace{P(\theta \, | \, D)}_{posterior} \propto \underbrace{P(\theta)}_{prior} \times \underbrace{P(D \, | \, \theta)}_{likelihood}\]

normalizing constant:

\[ \int P(\theta') \times P(D \mid \theta') \, \text{d}\theta' = P(D) \]

problem

how to calculate for unwieldy models with high-dimensional \(\theta\)?

notation

• \(X = (X_1,\dots,X_k)\) is a vector of random variables
• true distribution of \(X\) is \(P\)

desideratum

an efficient way of getting samples \(x \sim P\) without access to \(P\) itself

intuition

• a sequence of elements from \(X\), \(x_0, x_1, \dots, x_n\) such that every \(x_{i+1}\) depends only on its predecessor \(x_i\)
  • think: probabilistic finite state machine

Markov property

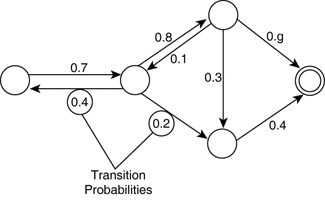
\[P(X_{n+1} = x_{n+1} \mid X_0 = x_0, \dots, X_n = x_n) = P(X_{n+1} = x_n \mid X_n = x_n)\]

idea

• get sequence of samples \(x\) s.t. every sample depends only on predecessor
• the stationary distribution of the chain is \(P\)
• in the limit, then, \(x\) are representative samples of \(P\), \(x \sim P\)

dummy

benefits & pitfalls

• set of islands \(X = \{x_1, x_2, \dots x_n\}\)
• goal: hop around & visit every island \(x_i\) proportional to its population \(P(x_i)\)
  • think: "samples" from \(x \sim P\)
• problem: island hopper can remember at most 2 islands' population
  • think: we don't know the normalizing constant

• let \(f(x) = \alpha P(x)\) (e.g., unnormalized posterior)
• start at random \(x^0\), define probability \(P_\text{trans}(x^i \rightarrow x^{i+1})\) of going from \(x^{i}\) to \(x^{i+1}\)
  • proposal \(P_\text{prpsl}(x^{i+1} \mid x^i)\): prob. of considering jump to \(x^{i+1}\) from \(x^{i}\)
  • acceptance \(P_\text{accpt}(x^{i+1} \mid x^i)\): prob of making jump when \(x^{i+1}\) is proposed \[P_\text{accpt}(x^{i+1} \mid x^i) = \text{min} \left (1, \frac{f(x^{i+1})}{f(x^{i})} \frac{P_\text{prpsl}(x^{i} \mid x^{i+1})}{P_\text{prpsl}(x^{i+1} \mid x^i)} \right)\]
  • transition \(P_\text{trans}(x^i \rightarrow x^{i+1}) = P_\text{prpsl}(x^{i+1} \mid x^i) \times P_\text{accpt}(x^{i+1} \mid x^i)\)

• motto: always up, down with probability \(\frac{f(x^{i+1})}{f(x^{i})}\)
• ratio \(\frac{f(x^{i+1})}{f(x^{i})}\) means that we can forget about normalizing constant
• \(P_\text{trans}(x^i \rightarrow x^{i+1})\) defines transition matrix -> Markov chain analysis!
• for suitable proposal distributions:
  • stationary distribution exists (first left-hand eigenvector)
  • every initial condition converges to stationary distribution
  • stationary distribution is \(P\)

• Metropolis is a very general and versatile algorithm
• however in specific situations, other algorithms may be better applicable
• for example, if \(X=(X_1,\dots,X_k)\) is a vector of random variables and \(P(x)\) is a multidimensional distribution
• in such cases, the Gibbs sampler may be helpful
• basic idea: split the multidimensional problem into a series of simpler problems of lower dimensionality

• assume \(X=(X_1,X_2,X_3)\) and \(p(x)=P(x_1,x_2,x_3)\)
• start with \(x^0=(x_1^0,x_2^0,x_3^0)\)
• at iteration \(t\) of the Gibbs sampler, we have \(x^{i-1}\) and need to generate \(x^{i}\)
  • \(x_1^{i} \sim P(x_1 \mid x_2^{i-1},x_3^{i-1})\)
  • \(x_2^{i} \sim P(x_2 \mid x_1^{i},x_3^{i-1})\)
  • \(x_3^{i} \sim P(x_3 \mid x_1^{i},x_2^{i})\)
• for a large \(n\), \(x^n\) will be a sample from \(P(x)\)
  • \(x^n_k\) will be a sample from \(P(x_k)\) (marginal distribution)

• Gibbs sampling can be more efficient than MH
• Gibbs needs samples from conditional posterior distribution
  • MH is more generally applicable
• preformance of MCMC algorithms depends on proposal distribution
• clever software helps determines which algorithm to use and how to fine-tune it

dummy dummy dummy

potential

kinetic

• momentum
  • e.g., standard deviation of Gaussian that determines initial jiggle

dummy

• step size
  • how big a step to take in discretization of gradient

dummy

• number of steps
  • how many steps before producing the proposal

convergence/representativeness

• we have samples from MCMC, ideally several chains
• in the limit, samples must be representative of \(P\)
• how do we know that our meagre finite samples are representative?

efficiency

• ideally, we'd like as small a sample set as possible
• how do we measure that we have "enough" samples?

\(\hat{R}\)-statistics

• a.k.a.:
  • Gelman-Rubin statistics
  • shrink factor
  • potential scale reduction factor
• idea:
  • compare variance within a chain to variance between chains
  • [think: ANOVA]
• in practice:
  • use software to compute it
  • aim for \(\hat{R} \le 1.1\) for all continuous variables

• intuition:
  • how many samples are "efficient, actual samples" if we strip off autocorrelation
• definition:

\[\text{ESS} = \frac{N}{ 1 + 2 \sum_{k=1}^{\infty} ACF(k)}\]

• declarative model specification
  • model as a directed acyclic graph / Bayes nets
    • nodes are variables, edges are deterministic or probabilistic dependencies
  • order invariant
  • no variable reassignment, no control flow statements etc.
    • exception: "ifelse" and "step" commands for boolean switching
    • "for"-loops for vector construction
• automatically selects adequate sampler
• call from & process output, e.g., in R via packages:
  • R2Jags
  • rjags
  • runjags

require('rjags')
modelString = "
model{
  theta ~ dbeta(1,1)
  k ~ dbinom(theta, N)
}"
# prepare for JAGS
dataList = list(k = 14, N = 20)
# set up and run model
jagsModel = jags.model(file = textConnection(modelString), 
                       data = dataList,
                       n.chains = 2)
update(jagsModel, n.iter = 5000)
codaSamples = coda.samples(jagsModel, 
                           variable.names = c("theta"),
                           n.iter = 5000)

require('ggmcmc')
require('dplyr')
ms = ggs(codaSamples)
ms %>% group_by(Parameter) %>% 
   summarise(mean = mean(value),
             HDIlow  = HPDinterval(as.mcmc(value))[1],
             HDIhigh = HPDinterval(as.mcmc(value))[2])

## # A tibble: 1 × 4
##   Parameter      mean    HDIlow   HDIhigh
##      <fctr>     <dbl>     <dbl>     <dbl>
## 1     theta 0.6814352 0.4967396 0.8756536

  tracePlot = ggs_traceplot(ms)  
  densPlot = ggs_density(ms) + 
    stat_function(fun = function(x) dbeta(x, 15,7), color = "black")

  require('gridExtra')
  grid.arrange(tracePlot, densPlot, ncol = 2) 

Your turn: what's this model good for?

• obs is a vector of 100 observations (real numbers)

model{
  mu ~ dunif(-2,2)
  var ~ dunif(0, 100)
  tau = 1/var
  for (i in 1:100){
    obs[i] ~ dnorm(mu,tau)
  }
}

NB: JAGS' precision \(\tau = 1/\sigma^2\), not standard deviation \(\sigma\) in dnorm

model{
  mu ~ dunif(-2,2)
  var ~ dunif(0, 100)
  tau = 1/var
  for (i in 1:100){
    obs[i] ~ dnorm(mu,tau)
  }
}

\[\mu \sim \text{Unif}(-2,2)\] \[\sigma^2 \sim \text{Unif}(0,100)\] \[obs_i \sim \text{Norm}(\mu, \sigma)\]

• mc-stan.org

• actively developed by Andrew Gelman, Bob Carpenter and others

• uses HMC and NUTS, but can do variational Bayes and MAP too

• written in C++

• cross-platform

• interfaces: command line, Python, Julia, R, Stata, Matlab

plot(stanFit)

codaSamples = As.mcmc.list(stanFit)
ms = ggs(stanFit)
ggs_density(ms)

problem

• Stan needs gradients / derivatives
  • cannot infer discrete latent parameters

dummy

solution

• marginalize out

15 people answered 40 exam questions. Here's their scores:

k <- c(21,17,21,18,22,31,31,34,34,35,35,36,39,36,35)
p <- length(k) #number of people
n <- 40 # number of questions

• assume that some guessed randomly, others gave informed answers
• who is a guesser?
• what's the probability of correct answering for non-guessers?

dummy dummy dummy dummy dummy dummy

k <- c(21,17,21,18,22,31,31,34,34,35,35,36,39,36,35)
show(summary(codaSamples)[[1]][,1:2])

##           Mean         SD
## phi   0.863443 0.01719438
## z[1]  0.000000 0.00000000
## z[2]  0.000000 0.00000000
## z[3]  0.000000 0.00000000
## z[4]  0.000000 0.00000000
## z[5]  0.000000 0.00000000
## z[6]  0.992200 0.08797689
## z[7]  0.994500 0.07396146
## z[8]  1.000000 0.00000000
## z[9]  0.999900 0.01000000
## z[10] 1.000000 0.00000000
## z[11] 1.000000 0.00000000
## z[12] 1.000000 0.00000000
## z[13] 1.000000 0.00000000
## z[14] 1.000000 0.00000000
## z[15] 1.000000 0.00000000

data { 
  int<lower=1> p;  int<lower=0> k[p];   int<lower=1> n;
}
transformed data {
  real psi; psi <- .5;
}
parameters {
  real<lower=.5,upper=1> phi; 
} 
transformed parameters {
  vector[2] log_alpha[p];
  for (i in 1:p) {
    log_alpha[i,1] <- log(.5) + binomial_log(k[i], n, phi);
    log_alpha[i,2] <- log(.5) + binomial_log(k[i], n, psi); 
  }
}
model {
  for (i in 1:p)
    increment_log_prob(log_sum_exp(log_alpha[i]));  
}
generated quantities {
  int<lower=0,upper=1> z[p];
  for (i in 1:p) {
    z[i] <- bernoulli_rng(softmax(log_alpha[i])[1]);
  }
}

log score

• \(\log P(D, \theta) = \log \left( P(\theta) \ P(D \mid \theta) \right ) = \log P(\theta) + \log P(D \mid \theta)\)
• log-score for one participant in our example:

\[\log P(k_i, n, z_i, \phi) = \log \text{Bern}(z_i \mid 0.5) + \log \text{Binom}(k_i, n, \text{ifelse}(z=1, \phi, 0.5))\]

marginalizing out

\[ \begin{align*} P(k_i, n, \phi) & = \sum_{z_i=0}^1 \text{Bern}(z_i \mid 0.5) \ \text{Binom}(k_i, n, \text{ifelse}(z=1, \phi, 0.5)) \\ & = \text{Bern}(0 \mid 0.5) \ \text{Binom}(k_i, n, 0.5)) + \\ & \ \ \ \ \ \ \ \ \ \ \text{Bern}(1 \mid 0.5) \ \text{Binom}(k_i, n, 1)) \\ & = \underbrace{0.5 \ \text{Binom}(k_i, n, 0.5))}_{\alpha_0} + \underbrace{0.5 \ \text{Binom}(k_i, n, 1))}_{\alpha_1} \\ \log P(k_i, n, \phi) & = \log \sum_{i=0}^1 \exp \log \alpha_i \end{align*}\]

library(rwebppl)
datainput = list(n = 24, k = 7)
modelString = ' 
var successes = dataFromR["k"][0];
var trials = dataFromR["n"][0];
var model2compute = function(){
  var p = uniform(0,1); 
  observe(Binomial({n: trials, p: p}), successes);
  return {bias: p}; }'
wp.rs = webppl(modelString, model_var = "model2compute", 
               data = datainput,
               data_var = "dataFromR",
               inference_opts = list(method = "MCMC",
                                     samples = 15000,
                                     burn = 5000, verbose = TRUE),
               output_format = "ggmcmc",
               chains = 2, cores = 2)

goals

- liberate psychology from expensive, proprietory software (SPSS)
- provide Bayesian statistical methods in an accessible way
- provide a universal platform for publishing statistical analysis with rich UIs